12.1 3D Coordinate Systems #

• Right hand rule: Index point to .$x$, thumb to .$z$, and write through .$y$
• If you have point .$P(a,b,c)$ and drop a perpendicular dot on the .$xy$-plane at .$a,b,0$, you now have a projection of .$P$ onto the .$xy$-plane
• The distance .$|P_1 P_2|$ between two points .$P_1(x_1, y_1, z_1)$ and .$P_2(x_2, y_2, z_2)$ is $$|P_1 P_2| = \sqrt{(x_2-x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$$
• We can define the equation for a sphere with a center at .$C(h,k,l)$ and radius .$r$ as $$(x-h)^2 + (y-k)^2 + (z-l)^2 = r^2$$

12.2 Vectors #

• Written as .$\overrightarrow{AB}$
• Has initial point .$A$ at the tail and the a terminal point .$B$ at the tip
  • If the initial point .$A$ is at .$(x_1, y_1, z_1)$ and terminal point .$B$ is at .$(x_2, y_2, z_2)$, then we can write .$\overrightarrow{AB} = \langle x_2 - x_1, y_2 - y_1, z_2 - z_1\rangle$
• Vectors with the same length/magnitude are called equivalent or equal, despite not necessarily having the same initial/termination points
• Vector addition (order doesn’t matter) $$ \overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{BC} + \overrightarrow{AB}$$ $$ \vec u - \vec v = \vec u + (- \vec v)$$ $$ \vec a + (\vec b + \vec c) = (\vec a + \vec b) + \vec c$$
• Vector multiplication
  • Given scalar .$c$ and vector .$\vec v$, .$c\cdot\vec v$ is like .$\vec v$ but with length changed by a factor of .$\Vert c\Vert$
  • If .$c<0$, then the vector is flipped around
  • $$c\cdot\vec v = \langle cv_x, cv_y, cv_z\rangle$$
• Magnitude for .$\vec a = \langle a_x, a_y, a_z \rangle$:
  • $$ \Vert \vec a \Vert = \sqrt{a_x^2 + a_y^2 + a_z^3}$$
• Unit vector
  • Has length of one
  • If .$\vec a \neq 0$ then the unit vector .$\vec u$ in the same direction as .$\vec a$ is:
    • $$\vec u = \frac{\vec a}{\Vert \vec a \Vert} = \frac{1}{\Vert \vec a \Vert} \vec a$$
    • Notice that .$\frac{1}{\Vert \vec a \Vert}$ is a scalar

12.3 Dot Product #

• The dot product measures the extent which two vectors are parallel to one another
  • Two vectors are perpendicular/orthogonal .$\perp$ (.$90^\circ$ from one another) iff the dot product is 0
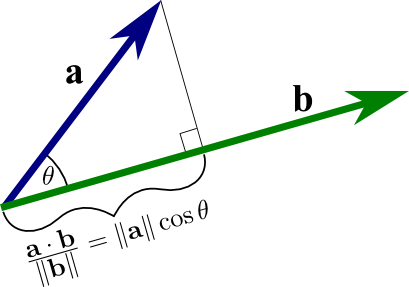
• .$\vec a \cdot \vec b$ is the length of .$\vec a$ times the scalar projection of .$\vec b$ onto .$\vec a$
• Notice that the dot product gives a scalar $$\langle a_1, a_2, a_3 \rangle \cdot \langle b_1, b_2, b_3 \rangle = a_1b_1 + a_2b_2 + a_3b_3$$

  $$\vec a \cdot (\vec b + \vec c) = \vec a \cdot \vec b + \vec a\cdot \vec c$$ $$ \vec a \cdot \vec a = \Vert \vec a \Vert ^2$$ $$ \vec a \cdot \vec b = \vec b \cdot \vec a $$ $$ (c \vec a) \cdot \vec b = c (\vec a \cdot \vec b) = \vec a \cdot (c \vec b)$$

  $$\vec a \cdot \vec b = \Vert\vec a\Vert\ \Vert\vec b\Vert \cos \theta$$ $$\Vert\vec a - \vec b \Vert^2 = \Vert\vec a\Vert^2+\Vert\vec b\Vert^2 - 2\Vert\vec a\Vert \Vert\vec b\Vert \cos\theta\ $$ $$… = \Vert\vec a\Vert\ \Vert\vec b\Vert \cos \theta$$ $$\cos\theta = \frac{\vec a \cdot \vec b}{\Vert\vec a\Vert\ \Vert\vec b\Vert}$$

  $$\cos \theta = \frac{\vec a}{\Vert \vec a \Vert} \cdot \frac{\vec b}{\Vert \vec b \Vert} \Longrightarrow \cos^{-1}\bigg(\frac{\vec a}{\Vert \vec a \Vert} \cdot \frac{\vec b}{\Vert \vec b \Vert} \bigg) = \theta $$

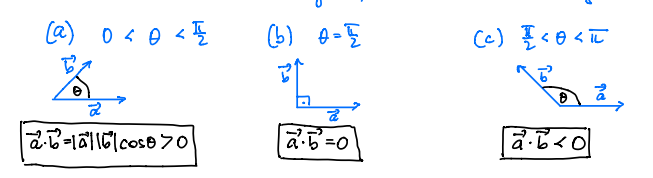
Direction Vectors #

• The direction angles of a nonzero vector .$\vec a$ are the .$\alpha, \beta, \gamma$ that a makes with the positive .$x,y,z$-axes respectively $$\cos\alpha = \frac{\vec a \cdot \vec i}{\Vert \vec a \Vert \Vert \vec i \Vert} = \frac{a_1}{\Vert \vec a \Vert}$$ $$\vec a = \Vert \vec a \Vert \langle \cos \alpha, \cos \beta, \cos \gamma \rangle$$

Projections #

• Scalar projection of .$\vec b$ onto .$\vec a$: $$\text{comp}_\vec a\vec b = \frac{\vec a\cdot\vec b}{\Vert\vec a\Vert}$$
• Vector projection of .$\vec b$ onto .$\vec a$: $$\text{proj}_\vec a\vec b = \bigg(\frac{\vec a\cdot\vec b}{\Vert\vec a\Vert}\bigg)\frac{\vec a}{\Vert\vec a\Vert} = \frac{\vec a\cdot\vec b}{\Vert\vec a\Vert^2}\vec a$$

12.4 Cross Product #

• The cross product measures how orthogonal two vectors are
  • Therefore, .$(\vec a \times \vec b) \cdot \vec b = 0$ because measures how similar (close to .$0^\circ$) two vectors are and cross product outputs a vector orthogonal (.$90^\circ$ to both .$\vec a, \vec b$)
  • Two nonzero vectors are only parallel iff their cross product is zero
  • The magnitude is also the area of a parallelogram formed by the two vectors
    • We can find the volume of the 3D parallelogram formed by three vectors with the following equation: $$\vec a \cdot (\vec b \times \vec c) = (\vec a \times \vec b) \cdot \vec c$$
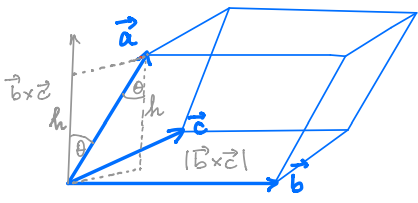
    • Realize that if the resulting area is .$0$, then all of the points exist on the same plane
• Notice that the cross product gives a vector that is orthogonal to both original vectors
  • Direction is determined with the right-hand rule
• We can also calculate the determinant with the unit vectors .$\langle \hat i, \hat j, \hat k \rangle$to find the cross product $$\langle a_1, a_2, a_3 \rangle \times \langle b_1, b_2, b_3 \rangle = \langle a_2b_3 - a_3 b_2, -(a1_b3 - a_3 b_1), a_1b_2 - a_2 b_1 \rangle$$ $$\vec a \times \vec b = \Vert \vec a \Vert \Vert \vec b \Vert \sin\theta$$ $$(\vec a \times \vec b) \times \vec c \neq \vec a \times (\vec b \times \vec c) \Longrightarrow \vec a \times (\vec b \times \vec c) = (\vec a \cdot \vec c) \vec b - (\vec a \cdot \vec b ) \vec c$$

  $$\vec a \times \vec b \neq \vec b \times \vec b \Longrightarrow \vec a \times \vec b = - \vec b \times \vec a$$ $$(c \vec a) \times \vec b = c(\vec a \times \vec b) = \vec a \times (c \vec b)$$

  $$\vec a \times (\vec b + \vec c) = \vec a \times \vec b + \vec a \times \vec c$$ $$(\vec a + \vec b) \times \vec c = \vec a \times \vec c + \vec b \times \vec c$$

  $$\Vert \vec a \times \vec b \Vert ^2 = \Vert \vec a \Vert^2 \Vert \vec b \Vert^2 - (\vec a \cdot \vec b)^2 = \Vert \vec a \Vert^2 \Vert \vec b \Vert^2 \sin^2 \theta$$ $$… \Longrightarrow \Vert \vec a \times \vec b \Vert \Vert \vec a \Vert \Vert \vec b \Vert \sin \theta$$

12.5 Equation of Lines and Planes #

Line #

• If given a point .$P_0 (x_0, y_0, z_0)$ and a vector .$\vec v = \langle a,b,c \rangle$ that passes through said point (parallel), we can write a line equation as: $$\langle x, y, z \rangle = P_0 + t \vec v = \langle x_0 + ta, y_0 +tb, z_0 + tc \rangle;\ \ t \in \mathbb{R}$$
• We can then isolate .$t$ to find the symmetric equation of the line $$ t = \frac{x-x_0}{a} = \frac{y-y_0}{b} = \frac{z-z_0}{c} $$
• And we can extrapolate this to write an equation we can use to verify if two points are on a line: $$ t = \frac{x-x_0}{x_1-x_0} = \frac{y-y_0}{y_1-y_0} = \frac{z-z_0}{z_1-z_0} $$
  • Note: If we have no change in an axis (such as .$x$), then .$x_1-x_0$ is zero. Therefore, we can write .$x = x_0$ (because we know it never changes) and the other relations for .$y$ and .$z$ still work
• We can also write our original equation in vector form as $$\vec r(t) = \vec r_0 + t\vec v$$
• Which we can use to write a specific line between point .$A$ and .$B$ from .$t \in [0,1]$ as $$\overrightarrow{AB} = \langle x_1 - x_0, y_1 - y_0, z_1 - z_0 \rangle$$ $$r(t) = \vec A(1-t) + \vec B(t)$$
• Two vectors are equal iff corresponding components are equal
• 3D Lines can be parallel (same direction vector), intersect at one point (.$r_1 = r_2\ @\ t_1, t_2$), or skew (not intersecting nor parallel – not possible in 2D)

Planes #

• Planes need a point and direction
  • Point .$P_0 (x_0, y_0, z_0)$ is trivial; a plane is a set of various points
  • Direction is described by the normal vector .$\vec n = \langle a,b,c \rangle$; only one normal unit vector per plane
    • Given three points .$P_1, P_2, P_3$ on the plane, we can write two vectors .$\vec a = \overrightarrow{P_1 P_2}, \vec b = \overrightarrow{P_1, P_3}$ as we can find the normal vector as .$\vec n = \vec a \times \vec b$
• Knowing this, we can write a vector equation: $$ \vec n \cdot \overrightarrow{P_0 P} = 0$$ $$ \vec n \cdot (\vec r - \vec r_0) = 0$$
• This can also be parameterized as both the scalar and linear equation respectively: $$a(x-x_0) + b(y-y_0) + c(z-z_0) = 0$$ $$ax + yz + cz + d = 0$$
• Planes are parallel if their normal vectors are parallel
• Otherwise, they intersect and form a straight line

Common Questions #

• Intersection point(s) of plane and parametric curve
  • Given parametric curve .$C = \langle \alpha + a\cdot t, \beta + b\cdot t, \gamma + c \cdot t \rangle$ and plane equation .$P = x + y + z + d = 0$ …
  1. Plug in each component of .$C$ as .$x,y,z$ in the .$P$ equation
  2. Solve for .$t$(s), then plug (it/them) into the prior equation to get intersection point(s)
• Angle between planes
  • Given two planes with .$\vec n_1, \vec n_2$ respectively
  1. Use .$\theta = \cos^{-1}\Big(\frac{\vec n_1 \cdot \vec n_2}{\Vert \vec n_1 \Vert \Vert \vec n_2 \Vert}\Big)$ to find .$\theta$
• Angle between parametric lines that intercept at point .$P_3$
  • Given parametric equations .$L_1 = P_1 + t\vec v_1$ and .$L_2 = P_2 + s\vec v_2$
  1. Find the .$t_3$ and .$s_3$ for when .$L_1 = P_3$ and .$L_2 = P_3$ (point of intersection)
  2. Use .$\theta = \cos^{-1}\Big(\frac{\vec v_1’(t_3) \cdot \vec v_2’(s_3)}{\Vert \vec v_1’(t_3) \Vert \Vert \vec v_2’(s_3) \Vert}\Big)$ to find .$\theta$
• Intersection of two lines:
  • .$L_1: \langle x_1, y_1, z_1 \rangle + t \cdot \langle a_1, b_1, c_1\rangle; L_2: \langle x_2, y_2, z_2 \rangle + s \cdot \langle a_2, b_2, c_2 \rangle;$
  • First, check if they are parallel by checking if the directions of the two lines are scalar multiples of one another.
  • Second, check if they intersect by setting the two parametric equations equal to one another:
    • .$x_1 + t a_1 = x_2 + s a_2; y_1 + t b_1 = y_2 + s b_2; z_1 + t c_1 = z_2 + s c_2$
    • If an equation exists (that is, there is a valid .$t$ and .$s$) then they intersect at .$L_1(t)$ or .$L_2(s)$
• Intersection line .$L$ of two planes
  1. Set one of the 3D variables to zero (e.x. .$z = 0$) to find where the two planes intersect the remaining plane (in this case the .$z$ plane)
  2. We find the intersection point .$P (\alpha, \beta, 0)$ by solving when our plane equations in the prior equation are equal
  3. Since the line .$L$ is orthogonal to both planes’ normal vectors, our direction vector is .$\vec v = n_1 \times n_2 = \langle a,b,c \rangle$
  4. We can then plug in everything into the symmetric equation: .$\frac{x-\alpha}{a} = \frac{y-\beta}{b} = \frac{z-0}{c}$
• Distance from point to plane
  • Given point .$P_1(x_1, y_1, z_1)$ and plane .$ax+by+cz+d = 0$ $$D = \Vert \text{comp}_{\vec n}{\vec b} \Vert = \frac{\vert ax_1 + by_1 + cz_1 +d\vert}{\sqrt{a^2 + b^2 + c^2}}$$
• Distance from skew line to skew line
  • Given .$L_1 = \langle x_1, y_1, z_1 \rangle + t \vec v_1$ and .$L_2 = …$
  1. Find the plane containing .$L_2$ that is parallel to .$L_1$. .$P_3 = \langle x- x_2, y - y_2, z - z_2 \rangle \cdot (v_1 \times v_2)$
  2. Find the .$D$istance from .$x_1, y_1, z_1$ on .$L_1$ to the plane .$P_3$ above $$D = \frac{\vert a_3 x_1 + b_3 y_1 + c_3 z_1 +d\vert}{\sqrt{a_3^2 + b_3^2 + c_3^2}}$$
• Distance from point to line
  • Given line .$L = \langle x_0, y_0, z_0 \rangle + \langle a, b, c \rangle$ and point .$P = \langle P_x, P_y, P_z \rangle$
  1. Write a distance equation as .$D^2 = ((x_0 + ta) - P_x)^2 + ((y_0 + tb) - P_y)^2 + ((z_0 + tc) - P_z)^2$
  2. Find the minimum value of .$t$ and plug in into the equation above and find .$D$ (but not .$D^2$!)

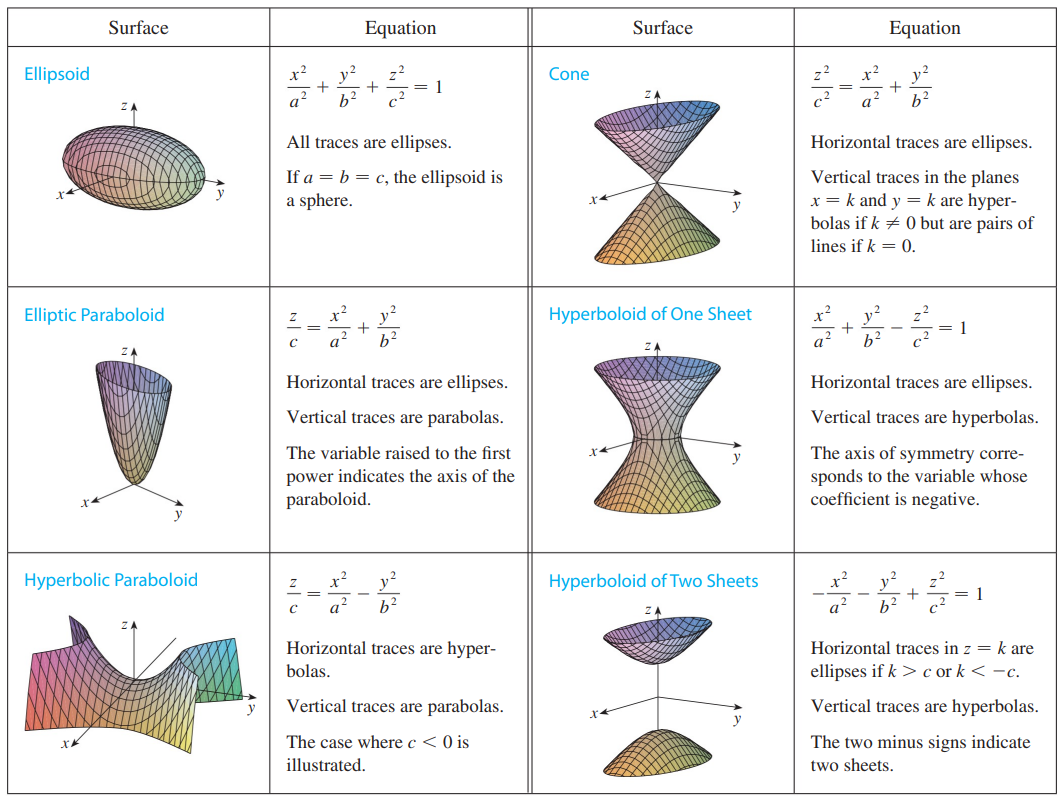
12.6 Cylinders and Quadratic Surfaces #

Traces #

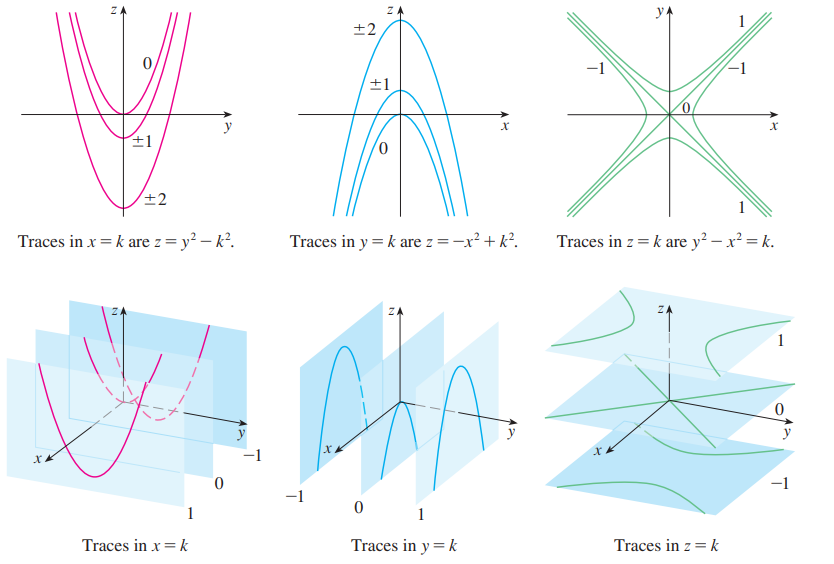
• Cross sections of a surface found by taking a three-variable equation and setting one of the equations variables equal to a constant.
• Help us visualize 3D curves by thinking about them from different axis

  $$z = \frac{x^2}{4} + \frac{y^2}{9} \Longrightarrow k = \frac{x^2}{4} + \frac{y^2}{9}$$

  $$… \Longrightarrow z = \frac{x^2}{4} + \frac{k^2}{9}$$

  • In the left example, for every .$z$ value we have a ellipse
  • In the right example, we have a parabola for every .$y$ value

Cylinder #

• A cylinder is a surface that consists of all rulings that at parallel to a given line that passes through a given plane curve
• Two variable equation in 3D space
  • E.x. .$y =\sin x, z = x^2$

Quadratic Surfaces #

• A quadric surface is the graph of a second-degree equation with three variables
• Two standard forms (when centered about origin): $$Ax^2 + By^2 + Cz^2 + J = 0$$ $$Ax^2 + By^2 + Iz = 0$$