25.1 The Electric Battery #
- Batteries produce electricity by transforming chemical energy into electric energy
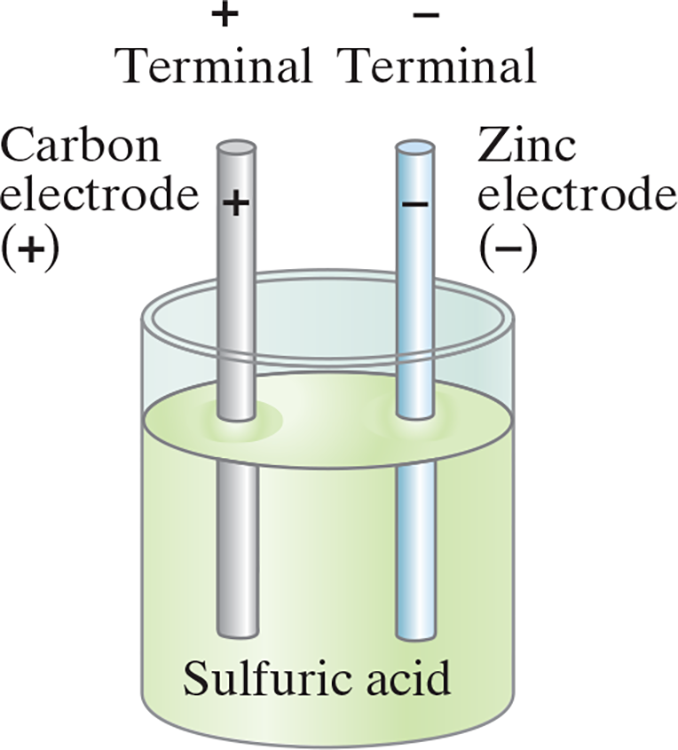
- Simple battery (cells) contain two plates or rods of dissimilar metals called electrodes
- The portion of rods outside of the solution are called the terminals
- Anode: The positive electrode
- Cathode: The negative electrode
- These electrodes are emersed in the electrolyte: a solution such as a dilute acid
Chemical Process:
- The acid dissolve the zinc electrode, causing zinc atoms to leave two electrons behind on the electrode and enters the solution as a positive ion. The zinc electrode thus acquires a negative charge.
- Then the electrolyte becomes positively charged and can pull electrons off the carbon electrode. Thus the carbon electrode becomes positively charged.
- Because there is an opposite charge on the two electrodes, there is a potential difference between the two terminals.
- When a battery isn’t connected, only a small amount of zinc is dissolved
- The zinc electrode becomes increasingly negative
- Thus, any new positive zinc ions produced are attracted back to the electrode
- That is, if a charge is allowed to flow then the zinc can dissolve
- The voltage depends ot the electrodes’ material and their relative ability to give up electrons
25.2 Electric Current #
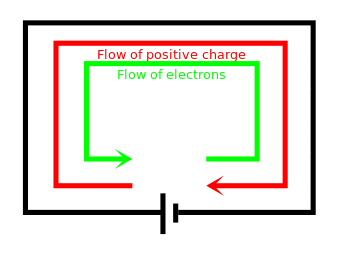
- When a circuit is formed, charge can move (flow) through the wires from one terminal to the other
- Any flow of charge is called an electric current
- Flow can only occur on a continuos conducting path (a complete circuit)
- If there’s any break, our circuit is called an open circuit and no current flows
- The symbol for battery is the following:
Conventional current from .$+$ to .$-$ is equivalent to a negative electron flow from .$-$ to .$+$
- Current in a wire is defined as the net amount of charge that passes through the wire’s full cross section at any point in time: $$\bar I = \frac{\Delta Q}{\Delta t} \Longrightarrow I = \frac{dQ}{dt}$$
- Current is measured in coulombs per second; ampere (amp): .$\text{1 A = 1 C/s}$
25.3 Ohm’s Law: Resistance and Resistors #
- For a current to exist, there must be a potential difference (e.g. between the terminals of a battery)
- That is, the current is proportional to the potential difference:
$$I \propto V$$
- E.x., a wire connected to a .$6V$ battery results in a current twice that of a .$3V$ battery
- The current depends on the resistance that the wires offers
- The electron flow is impeded partly due to the atoms in the wire
- .$R$ is this proportionality factor between voltage and current
- Thus, we get Ohm’s Law: $$V = IR$$
- Ohm’s law only works for when .$R$ is a constant, i.e a metal conductor
- In reality, .$R$ isn’t constant if temperature changes much
- Materials that follow Ohm’s law are labeled as “ohmic”
- Resistance has the units/notation .$\text{1 $\Omega$ = 1 V/A}$
- Resistors are used to limit/control the current in a circuit
- toolbox.mehvix.com/resistor
- As a current passes through a resistor, the charge/current stays the same but the electric potential decreases
Clarifications of Behavior
- Current’s magnitude depends on that device’s resistance
- Can be though of as the “response” to the voltage: increases if voltage increases or resistance decreases
- Current is constant – it’s energy so it cannot be destroyed by components and it’s not created by a battery
- Resistance is a property of the device/wire
- Voltage is external to the wire of device – it’s applied across the two ends of the wire
- Batteries maintain a constant potential difference – act as a source of voltage
25.4 Resistivity #
- Resistivity has experimentally been found as
$$R = \rho \frac{l}{A}$$
- .$\rho$ is the resistivity (constant of proportionality) and depends on the material
- Has units .$\Omega \cdot \text{m = V/A $\cdot $ m}$
- .$l$ is the wire length
- .$A$ is the cross-section area
- .$\rho$ is the resistivity (constant of proportionality) and depends on the material
- The reciprocal of resistivity is conductivity: .$\sigma = \rho^{-1}$
Temperature #
- Resistivity varies (generally increasing) with temperature
$$\rho_T = \rho_0 = \bigg[ 1+ \alpha (T-T_0)\bigg]$$
- .$\rho_0$ is the resistivity at some reference temperature .$T_0$ (i.e .$0^\circ \text{ C}$)
- .$\rho_T$ is the new resistivity at the current (higher) temperature .$T$
- .$\alpha$ is the temperature coefficient of resistivity that depends on material
- Note that the temperature coefficient for semiconductors can be negative.
- At higher temperatures, some of the electrons that are normally not free in a semiconductor can become free and contribute to the current.
- Thus, the resistance of a semiconductor can decrease with an increase in temperature.
25.5 Electric Power #
- Electric energy is transformed into thermal energy (and light) in stove burners, toasters, etc.
- The current creates collisions between the moving electrons and the atoms in the wire
- That is, the KE from the wire’s atoms increases meaning the temperature increases too
$$P = \frac{dU}{dt} = \frac{dq}{dt}\cdot V$$
- This is because energy is transformed when a tiny charge .$dq$ moves through a potential difference .$V$ is .$dU = V\ dq$
- The charge that flows per second, .$dq/dt$, is the electric current .$I$:
$$P = IV = I^2 R = \frac{V^2}{R}$$
- The SI unit for power is the watt: .$\text{1 W = 1 J/s}$
- We get the last two equations by plugging in .$V = IR$
25.7 Alternating Current #
- When a battery is connected to a circuit, the current moves steadily in one direction (DC: Direct Current)
- Electric generators at power plants produce AC: alternating current
- Reverses direction many times per second and is commonly sinusoidal $$V = V_0 \sin(2\pi ft) = V_0 \sin(\omega t)$$
- .$\omega$ = .$2\pi f$
- .$f$ is the frequency: number of complete oscillations per second
- Commonly .$\text{60 Hz}$ in NA
- Potential .$V$ oscillates between .$\pm V_0$, the peak voltage
- Current equation still works:
$$I = \frac{V}{R} = \frac{V_0}{R}\sin\omega t = I_0 \sin\omega t$$
- .$I_0 = V_0/R$ is the peak current
- Avg current is 0; it’s positive and negative for an equal amount of time
- Doesn’t mean that no heat is created or no power is needed
- Electrons are still moving though!
- Power is also consistent
$$P = I^2R = I_0^2 R \sin\omega t = \frac{V_0^2}{R} \sin\omega t$$
- Power is always positive because current is squared
- Since the .$\sin\dots$ oscillates between 1 and 0, the average power is $$\overline P = \frac{1}{2}I_0^2R = \frac{1}{2} \frac{V_0^2}{R}$$
- This can also be calculated by using the RMS values for .$I$ and .$V$ $$I_\text{rms} = \sqrt{\overline I^2} = \frac{I_0}{\sqrt{2}} \approx 0.707 I_0$$ $$V_\text{rms} = \sqrt{\overline V^2} = \frac{V_0}{\sqrt{2}} \approx 0.707 V_0$$ $$\dots \Longrightarrow \overline P = I_\text{rms} V_\text{rms} = I_\text{rms}^2 R = \frac{V_\text{rms}^2}{R}$$
- Fun fact: we can use the rms of a value to find the peak of it, e.x. $$V_0 = \sqrt{2} V_\text{rms}$$
- Keep in mind that this is the average power. Instantaneous power varies from .$0$ to .$2\overline P$
25.8 Microscopic View of Current #
- We’ve seen that electric current can be carried by negatively charged electrons in metal wires, and that in liquid solutions current can also be carried by positive and/or negatively charged ions
- When a potential difference is applied to the two ends of a wire, the direction of the electric field .$\vec E$ is parallel to the walls of the wire
- This field within the conducting wire does not contradict our earlier result that .$\vec E = 0$ inside a conductor in the electrostatic case, as we are no longer dealing with the static case.
- That is, charges are free to move in a conductor, and hence can move under the action of the electric field.
- If all the charges are at rest, then .$\vec E = 0$

- If all the charges are at rest, then .$\vec E = 0$
Current Density #
- Current density, .$\vec j$, is the current per area
$$j = \frac{I}{A} \Longrightarrow I = \int \vec j \cdot d \vec A$$
- .$I$ is the current through the whole surface
- .$d\vec A$ is an element of surface area over which the integration is taken
- Direction of the density is the same direction as .$\vec E$ – the direction that a positive charge would move
Drift Speed #
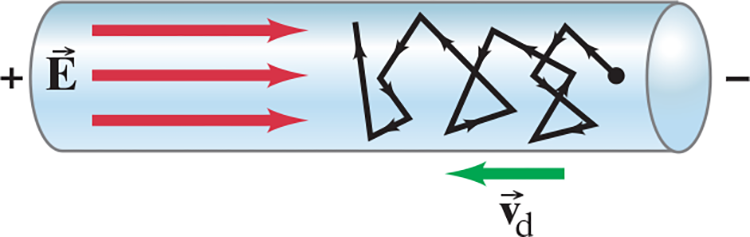
- Inside a wire, we can imagine the free electrons as moving about randomly at high speeds, bouncing off the metal atoms of the wire
- Somewhat like the molecules of a gas
- When an electric field exists in the wire the electrons feel a force and initially begin to accelerate but they soon reach a more or less steady average speed, known as their drift speed .$v_d$
- Collisions with atoms in the wire keep them from accelerating further
- The drift speed is normally very much smaller than the electrons’ average random speed inside the metal wire
Black zagged line represents the motion of an electron in a metal wire due to an electric field. The field .$\vec E$ gives electrons in random motion a net drift velocity .$\vec v_d$. Its direction (the net charge flow) is in the opposite direction of .$\vec E$ because electrons have a negative charge and .$\vec F = q \vec E$
- We can relate drift speed with the macroscopic view:
- In some time, the electrons travel (the average) distance .$l = v_d \Delta t$
- In that same time, electrons in volume .$V = Al = A v_d \Delta t$ pass through area .$A$ of the wire
- If there are .$n$ free electrons each of charge .$-e$ per unit volume, then the total electrons is .$N = nV$
- Thus, the charge is $$\Delta Q = \text{(number of charges, $N$)$\times$(charge per particle, $-e$)}$$ $$\dots = (nV)(-e) = -(nAv_d\Delta T)(e)$$
- We can then easily find the current (density): $$I = \frac{\Delta Q}{\Delta t} = -neAv_d$$ $$j = \frac{I}{A} = -nev_d$$
- Notice that the negative sign indicates that the direction of (positive) current flow is opposite to the drift speed of electrons.
Field inside a Wire #
- Voltage can be written in terms of microscopic values (in addition to the macro: .$V = IR$)
- Recall that resistance is related to density by .$R = \rho \frac{l}{A}$
- We can then write .$V$, .$I$ and .$j$ as
$$V = El = IR = (jA)\bigg(\rho \frac{l}{A}\bigg) = j \rho l$$
$$I = jA$$
$$j = \frac{1}{\rho}E = \sigma E$$
- .$\sigma$ is the conductivity of the wire
- .$\rho, \sigma$ do not vary with .$V$ and thus neither .$E$
- We can then write the microscopic statement of Ohm’s Law: $$\vec j = \sigma \vec E = \frac{\vec E}{\rho}$$
25.9 Superconductivity #
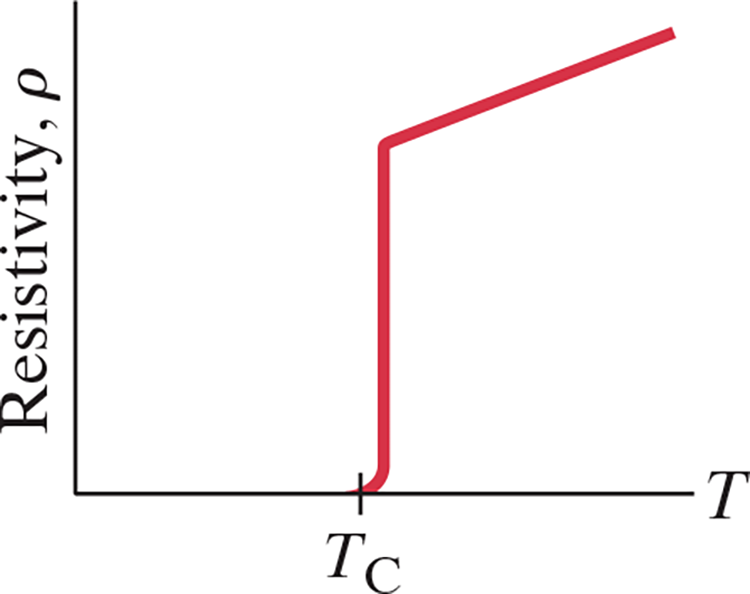
- At very low temperatures, the resistivity of certain metals and certain compounds or alloys becomes zero
- Materials in such a state are said to be superconducting
- In general, superconductors become superconducting only below a certain transition (critical) temperature, .$T_C$