19.1 Heat as Energy Transfer #
Units #
- Heat unit is calorie (cal)
- The amount of heat needed to raise the temperature of 1 gram of water by 1 celsius $$4.186 \text{ J} = 1 \text{ cal}$$
- Kilocalorie (kcal, Calorie) is more common
- Amount of heat needed to raise 1 kg of water by 1 celsius $$4.186 \text{ kJ} = 1 \text{ kcal}$$
- British system of units has British thermal units (Btu)
- One Btu is the heat needed to raise the temperature of 1 lb of water by 1 Fahrenheit $$1 \text{ Btu} = 0.252 \text{ kcal} = 1056 \text{ J}$$
- Gas companies use the unit therm: .$10^5 \text{ Btu}$
Heat #
- Heat is energy transferred from one object to another because of a difference in temperature.
- Energy transfers from hot to cold object until equilibrium
- The SI units for heat is the joule: this is because heat is a form of energy!
19.2 Internal Energy #
- Internal Energy: The sum of all the energy of all the molecules in an object
- Sometimes called thermal energy
Difference between Temp, Heat, and Internal Energy #
- Temperature is the average kinetic energy of all of the molecules
- Internal energy is the sum of the energy of all of the molecules
- E.x. Two equal-mass iron ingots could the same temperature as a single ingot, but the two would have double the internal energy
- Heat refers to the transfer of energy from one object to another due to a difference in temperatures
- Direction of transfer depends on temperature, not internal energy
- E.x. .$50\text{ g}$ of .$30^\circ\text{ C}$ water mixed with .$200 \text{ g}$ of .$25^\circ \text{ C}$ water results with heat transferring from the smaller sample with less internal energy to the larger sample with more internal energy.
Calculating Internal Energy #
- Internal energy is the sum of all the translational kinetic energy of the molecules in a monatomic gas
- Monatomic: Gas with one atom per molecule
- We can re-write this as the average KE per molecule times the total number of molecules, .$N$ $$E_{\text{int}} = N \bigg(\frac{1}{2}m\bar{v}^2\bigg) = \frac{3}{2}Nk_B T = \frac{3}{2}nRT$$
- We can see that internal energy for a monatomic gas depends only on the temperature and number of moles
- If a gas isn’t monatomic, then we need to consider the rotational and vibrational energy of the molecules
- Non-monatomic gasses result in a internal energy at a given temperature compared to a monatomic
- The internal energy of real gases depends mainly on temperature
- There are some exceptions of gases depending on pressure and volume as well
- Internal energy of liquids and solids is more complex
- It includes electric potential energy of the chemical bonds
19.3 Specific Heat #
- Amount of heat required to change the temperature of a material is found with the following:
$$\Delta Q = mc \Delta T$$
- .$c$ specific heat capacity that depends on the material .$[\text{J}/(\text{C}^\circ\text{ kg})]$
- For water at .$15 ^\circ \text{ C}$ and constant pressure .$1 \text{atm}$, .$c = 4168 \text{ J}/(\text{C}^\circ\text{ kg}) = 1.00 \text{ kcal}/(\text{C}^\circ \text{ kg})$
- .$c$ does vary to some extent with temperature (and slightly pressure), but for small .$\Delta T$ we can say .$c$ is a constant
- Relative to other materials/substances, water has a high specific heat capacity
19.4 Calorimetry #
Types of Systems #
- System: Any (set of) object(s) we choose to consider
- Closed System: Mass is constant, but energy may be exchanged within environment
- Isolated: If no energy in any form passes across its boundaries
- We idealize systems to be closed systems, which is rare in the real world
- Heat will flow from hot to cold region of system until equilibrium
- We can assume that no energy is lost; heat lost in one part = heat gained in another part or .$\Sigma Q = 0$
- Open System: Mass and energy may enter/leave
Calorimeter #
- Calorimetry: Quantitative measure of heat exchange
- Calorimeter tend to have insulation so that no heat is exchanged with the surrounding air
- Often use thermometer to measure change the temperature
- E.x. a substance sample will be heated up, measured, then quickly placed inside cool water of calorimeter
- The heat lost from the sample will be gained by the water and the calorimeter cup
- Measuring final temperature of the mixture lets us calculate the specific heat
- Assume that small masses like the thermometer/stirrer are negligible
19.5 Latent Heat #
- Change of Phase: When a material changes from solid to liquid or liquid to gas.
- A certain energy is required for a phase change
- During phase changes, temperature stops increasing and all energy goes into the phase change
- Latent heat is lost during phase change (often in the form of heat)
- Heat of fusion
- .$L_F$: Heat required to change .$1.0 \text{ kg}$ of a substance from solid to liquid state
- Heat fusion of water is .$79.7 \text{kcal/kg} = 333 \text{kJ/kg}$
- Heat of Vaporization
- .$L_V$: Heat required to change a substance from liquid to vapor phase
- Heat vaporization is .$539 \text{kcal/kg} = 2260 \text{kJ/kg}$
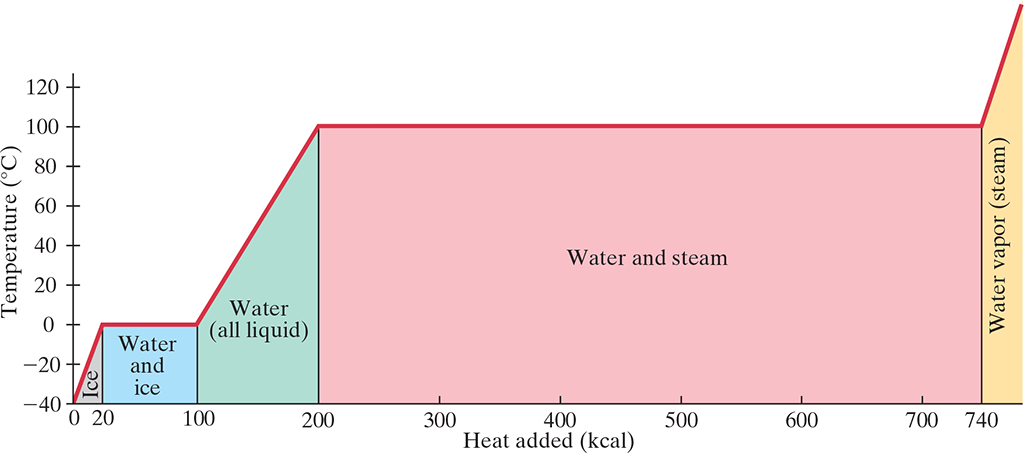
- Heat involved in the phase change depends on the mass and latent heat: $$\Delta Q = mL$$
- Therefore, when considering the change in a system involving heating a substance to a phase change (e.g. boiling at temperature .$T$), we can write:
$$\Delta Q_{\text{total}} = m_L c \Delta T + m_S L$$
- .$m_L$ is the total mass of the substance before the phase change (e.x. initial mass of substance, don’t subtract amount that vaporized)
- .$m_S$ is the mass of the substance that underwent a phase change (e.x. mass that vaporized)
Evaporation #
- Heat of Vaporization of water increases slightly with a decrease in Temperature
- At .$20^\circ \text{ C}$, it’s .$585 \text{ kcal/kg}$
- When liquid evaporates, the remaining liquid cools because the heat/energy comes from the water itself
- Therefore, internal energy decreases with evaporation
Kinetic Theory of Latent Heats #
- At melting point, the latent heat of fusion doesn’t increase the average KE / temperature
- Rather, the energy goes into overcoming the PE associated with the forces between the molecules
- Once the molecules in a solid are broken from there lattice formation, they can freely roll over one another as a liquid
- More energy is required for liquid to gas phase because the average distance between the molecules is greatly increased
- The larger the distance that the molecules have to be separated, the more work has to be done to pull them apart
19.6 First Law of Thermo #
- Heat and work are different
- Heat is the transfer of energy due to a difference in temperature – hot/cold bath around gas chamber
- Work is the transfer of energy not due to a temperature difference – piston applying force to a gas
- Internal energy and temperature are both proportional to heat and work though with the First law equation:
$$\Delta E_{\text{int}} = Q - W = E_{\text{int, 2}} - E_{\text{int, 1}} \ \ \ \text{[First Law of Thermo.]}$$
- .$W$ is net work done by the system
- Work done by system is .$\texttt{+}$
- Work done on the system is .$\texttt{-}$
- Gas expands .$\Longrightarrow$ sys looses energy
- .$Q$ is net heat added to the system
- Heat added is .$\texttt{+}$
- Heat lost is .$\texttt{-}$
- Gas is heated .$\Longrightarrow$ sys gains energy
- .$W$ is net work done by the system
- .$Q$ and .$W$ are not state variables in that a static state doesn’t have “heat” or “work” – only when the system changes through thermodynamic process can we measure heat/work.
- This is unlike .$P, V, T$ and .$E_{\text{int}}$ which are state variables (can be measured at all states)
- We can also extend the first law to include systems that have KE and PE: $$\Delta K + \Delta U + \Delta E_{\text{int}} = Q - W = E_{\text{int, 2}} - E_{\text{int, 1}}$$
19.7 Thermodynamic Process and the 1st Law #
Isothermal Process (.$\Delta T = 0$) #
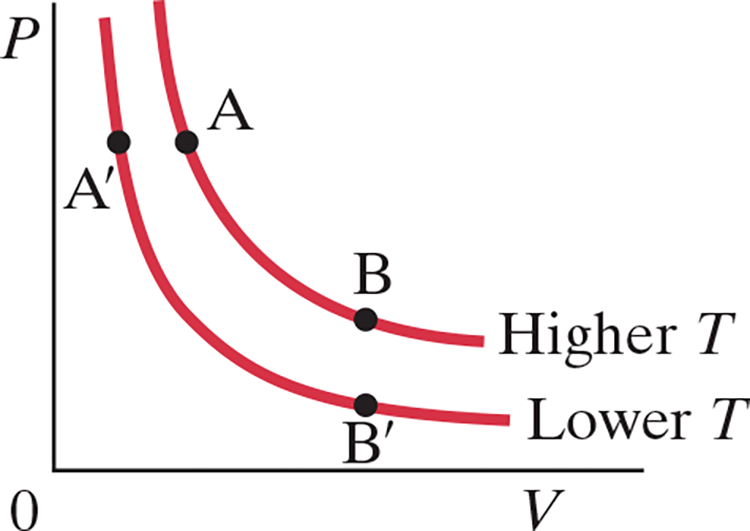
- When temperature is constant, .$PV$ is constant too
- Each label of points in the graph above represent the systems states (it’s pressure and temperatures)
- Isotherms: curves in PV diagram
- At a lower temperature, an isothermal process would be represented by the isotherm .$A’B'$
- We also assume that the container is a heat reservoir: a body whose mass is so big that the temperature doesn’t change when heat is exchanged
- We increase internal energy by doing work, such as by decreasing the volume of the container with by applying a force to a piston over some distance
- We assume that expansion/compression is quasistatic: we decrease the volume slow enough that we can consider it a series of equilibrium states all at the same temperature
- E.x. if we started with state .$A$ and added heat .$Q$ to the system, the system would reach point .$B$
- If .$T$ remain constant, the volume will expand, both doing work .$W$ on the environment and decreasing the .$P$
- We know .$E_\text{int} = \frac{3}{2}nR\Delta T$, and since .$\Delta T = 0 \Longrightarrow E_\text{int} = 0$
- Thus, .$E_\text{int} = Q - W \Longrightarrow W = Q$
$$$$ $$$$ $$W = \int_{V_A}^{V_B} P \ dV$$ $$… = nRT \int_{V_A}^{V_B} \frac{dV}{V}$$ $$… = nRT \ln{\frac{V_B}{V_A}}$$
Adiabatic Process (.$\Delta Q = 0$) #
- No heat allowed to flow in our out of system. This can happen if…
- Process happens so quickly that heat, a slow process, has no time to flow in/out
- E.x. a combustion engine happens quickly it’s nearly adiabatic
- System is well insulated
- Process happens so quickly that heat, a slow process, has no time to flow in/out
- If a system experiences an adiabatic process slowly, it will look similar to curve .$AC$
- Since .$Q = 0 \Longrightarrow \Delta E_\text{int} = -W$
- In a reverse processes represented by .$CA$ (adiabatic compression), work is done on the gas so .$E_\text{int}$ and .$T$ rise
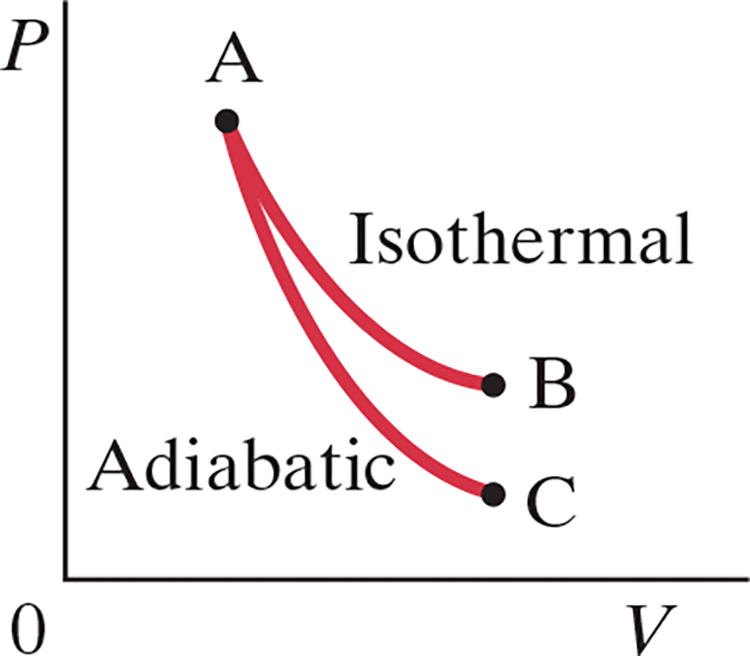
$$$$ $$$$ $$W = \int_{V_A}^{V_B} P \ dV$$ $$… = P_A V_A ^\gamma \int_{V_A}^{V_B} \frac{1}{V^\gamma}\ dV$$ $$… = \frac{P_A V_A - P_B V_B}{1-\gamma}$$
19.9 Adiabatic Expansions #
- The .$PV$ curve for adiabatic expansion (.$Q = 0$) is slightly less steep than isothermal processes (.$\Delta T = 0$)
- This means that for the same change in volume, the pressure will be greater in adiabatic processes
- Therefore, the temperature of a gas must drop in adiabatic expansion and rise in adiabatic compression
- Likewise, if during an adiabatic process the volume increases then the internal energy must decrease
- We can relate .$P$ and .$V$ for a quasistatic expansion / compression with
$$PV^\gamma = \text{[constant] for } \gamma = \frac{C_P}{C_V} = 1 + \frac{R}{C_V}$$
…which can also be written as the following (with .$d$ = degrees of freedom)
$$T_A^{C_V/R} V_A = T_B^{C_V/R} V_B$$
$$C_V = \frac{d}{2}R$$
$$C_P = \frac{d+2}{2}R$$
$$\gamma = \frac{d+2}{d}$$
Free Expansion #
- A type of adiabatic process where gas is allowed to expand in a volume without doing any work
- Must be done with insulated containers so that no heat is able to flow in/out; .$Q = 0$
- No work is done either because no object is moved; .$W = 0$
- Thus, .$\Delta E_\text{int} = 0$ and .$\Delta T = 0$
- In reality, we see temperature slightly drops meaning internal energy does depend on pressure or volume as well as temperature.
Isobaric and Isovolumetric .$(\Delta P = 0, \Delta V = 0)$ #
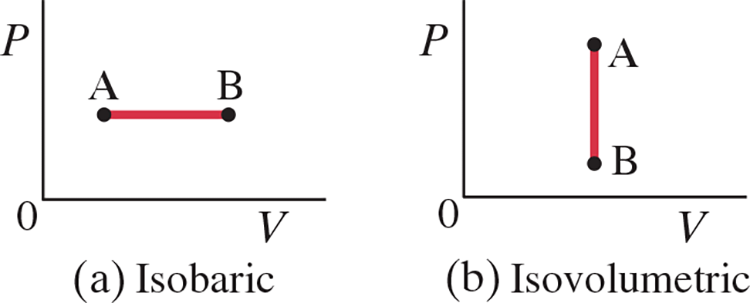
- Isobaric: .$\Delta P = 0 \Longrightarrow Q = \Delta E_\text{int} + W = \Delta E_\text{int} + P\Delta V$. The heat transferred to the system does work, but also changes the internal energy of the system
- Isovolumetric: .$\Delta V = 0 \Longrightarrow W = 0 \Longrightarrow Q = \Delta E_\text{int}$. The thermodynamic process is the addition or removal of heat.
- First law of thermo holds for both of these processes
$$$$ $$$$ $$W_{\text{Isovol.}} = 0$$ $$W_{\text{Isobaric}} = \int_{V_A}^{V_B} P \ dV$$ $$… = P \Delta V$$ $$… = P_B(V_B - V_A)$$ $$… = nRT_B(1 - \frac{V_A}{V_B})$$
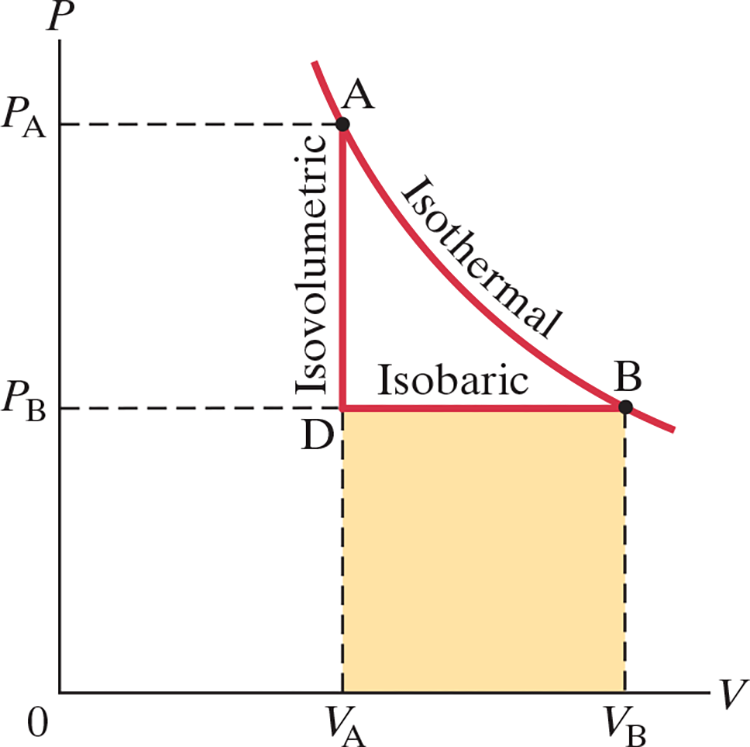
Work done in volume changes .$(\Delta V \neq 0)$ #
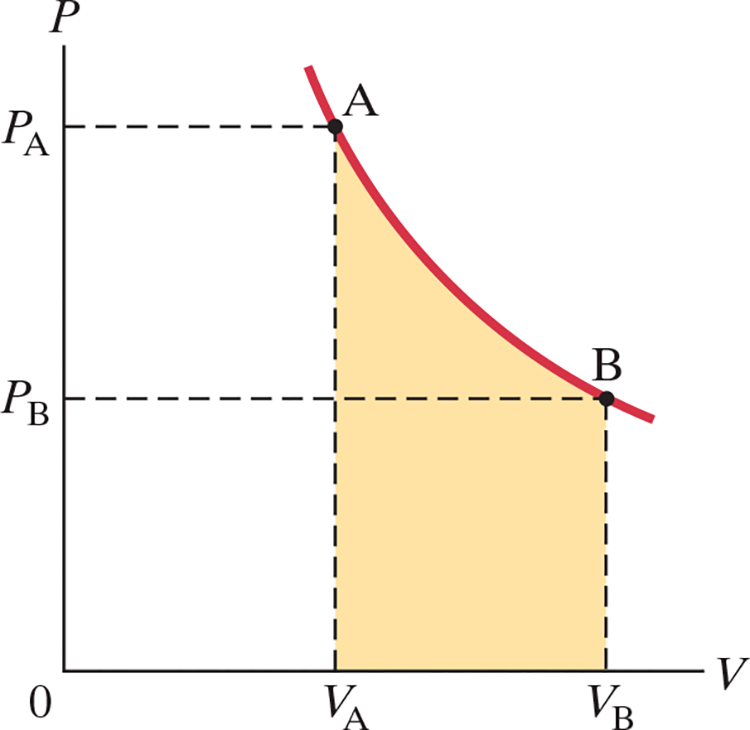
- For quasistatic processes: $$dW = \vec{F} \cdot d\vec{l} = PA d\vec{l} = P\ dV \ \ \ \text{(1)}$$ $$W = \int dW = \int_{V_A}^{V_B} P\ dV \ \ \ \text{(2)}$$
- .$\text{(1)}$ Where .$F = PA$ is the force the gas exerts on the piston and .$d\vec{l}$ is the (small) distance the piston moves
- .$\text{(2)}$ This shows that the work done is the area under the .$PV$ curve
- This equations are valid for work done in any volume change (solid, liquids, gas)
- .$W$ (and even .$Q$) depends on the initial and final states and also on the process (or path)
19.8 Molar Specific Heats for Gases and Equipartition of Energy #
Molar Specific Heat #
- Specific heat for gases depends heavily on the process and how it’s carried out
- Specific heat for constant pressure and constant volume vary
- We use molar specific heat for gases: .$C_V$ and .$C_P$ which are defined as the heat required to raise .$1 \text{ mol}$ of gas by .$1^\circ \text{ C}$ at a constant volume or pressure respectively.
- We then use .$n$ instead of .$m$ in our heat equations:
$$\Delta Q = nC_V \Delta T = mc_V \Delta T\ \ \ \text{[Constant Volume]}$$
$$\Delta Q = nC_P \Delta T = mc_P \Delta T\ \ \ \text{[Constant Pressure]}$$
which we can then relate to the specific heat with .$M$ as the molecular mass of the gas, .$m/n$ in grams/mol:
$$C_V = Mc_V$$
$$C_p = Mc_p$$
- In a heating process, when .$\Delta V = 0$ then the heat added, .$Q_V$ goes entirely into internal energy: .$Q_V = \Delta E_\text{int}$
- However, when pressure is constant work is done. Thus, heat added, .$Q_P$, goes towards increasing internal energy and work: .$W = P\Delta V$
- Therefore, more heat is needed for a constant pressure system: .$Q_P = \Delta E_\text{int} + P\Delta V$
- Since .$\Delta E_\text{int}$ is the same for both processes, we can write .$Q_P - Q_V = P \Delta V$
- With an ideal gas, we know .$V = nRT/P$ so .$\Delta V = nR\Delta T/P$ which we can combine with the prior equations to get: $$nC_P\Delta T - nC_V \Delta T = P\bigg(\frac{nR\Delta T}{P}\bigg) \Longrightarrow C_P - C_V = R$$
- We can also relate internal energy to molar specific heat for gases at constant volumes: $$\Delta E_\text{int} = Q_V \Longrightarrow \frac{\text{[Deg. of Freedom]}}{2}nRT = nC_V\Delta T \Longrightarrow C_V = \frac{3}{2}R$$
- We can then plug in our new value for .$C_V$ into the second to last equation .$C_P - C_V = R$ to get .$C_P = \frac{5}{2}R$ for a monatomic gas.
- We can also combine our equations to write a relation between internal energy and temperature again: $$\Delta E_\text{int} = nC_V \Delta T$$
Equipartition of Energy #
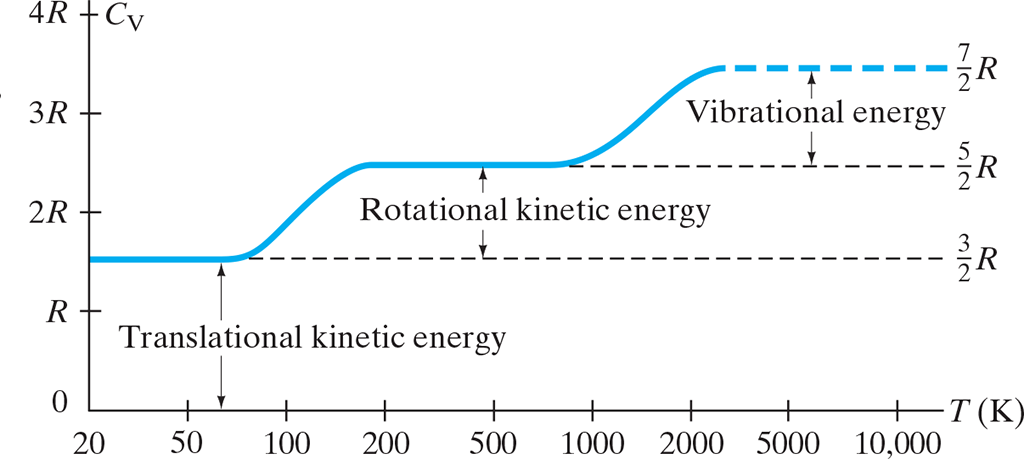
- Degrees of Freedom: The number of independent ways a molecule can posses energy
- Degrees of freedom depend on the temperature
- At low temperatures, the only degree of freedom is from translational .$KE$
- Starting after .$0K$
- Diatomic gas: .$C_V = \frac{3}{2}R$ (3 for each axis)
- Sum of .$\frac{1}{2}m \langle v_x, v_y, v_z \rangle$
- At “regular” temperatures, the molecules posses rotation energy
- Around .$50K$
- Diatomic gas: .$C_V = \frac{5}{2}R$
- Sum of .$\frac{1}{2}I \langle 0, \omega_y, \omega_z \rangle$ (since it’s rotating about .$\hat x$ meaning .$E_{\text{rotational, }x}) = 0$
- At higher temperatures, the molecules gain energy associated with their vibrations:
- Around .$1000K$
- One from KE of the molecules vibrating back and forth: .$\frac{1}{2}mv_{\text{COM}}^2$
- The second from PE of the vibrational motion (think of this as a spring’s PE): .$\frac{1}{2}kx^2$
- Solids:
- The molar temperature of solids at high temperatures is close to .$3R$.
- At high temperatures, there are six degrees of freedom: three from vibrational KE in the .$x, y,$ and .$z$ axis and three more from spring PE in the same axis
- Some of these degrees of freedom aren’t active at lower temperatures
- Principle of Equipartition of Energy: Energy is shared equally among degrees of freedom and each degrees has energy .$\frac{1}{2}k_B T$
- Thus, for a particle with three degrees of freedom (such as a monatomic gas) .$C_V = \frac{3}{2}R$
- Diatomic gases have five degrees so they have .$C_V = \frac{5}{2}R = 4.97 \text{ cal/(mol K)}$ and have .$E_\text{int} = N(\frac{5}{2}k_B T) = n C_V \Delta T = \frac{5}{2}nRT$ where .$n$ is the number of moles and .$N$ is the number of molecules
19.10 Heat Transfer #
Conduction #
- Heat transfer by contact
- Conduction can be visualized thinking of molecular collisions
- The hot end of an object has fast moving molecules
- These molecules bump into other molecules, transferring them some of their own KE
- This keeps repeating down the object
- Free electrons are the primary source of these collisions
- Heat conduction only occurs when there is a difference in temperatures
- Heat conduction rate is proportional to the difference in temperatures: $$\frac{\Delta Q}{\Delta t} = - kA\frac{T_1 - T_2}{l}$$
- Where .$A$ is the cross section area, .$l$ is the distance between the two ends, and .$k$ is a constant called thermal conductivity that depends on the material
- Good insulator / poor thermal conductors have a low .$k$
- Metals have .$k>1$
- Wood, plastics have small .$k$s
- Building materials sometimes list the thermal resistance, .$R$, which is equal to .$R = \frac{l}{k}$ where .$l$ is the material’s thickness
- Larger .$R$ means better insulation
- Good insulator / poor thermal conductors have a low .$k$
- If .$k$ or .$A$ isn’t constant, we consider a small thickness: $$ \frac{dQ}{dt} = -kA \frac{dT}{dx}$$
- .$\frac{T_1 - T_2}{l} \text{ and } \frac{dT}{dx}$ are called the temperature gradients
- We have a negative sign in the equation above because the direction of heat flow is opposite to the temperature gradient
- A steady system state is reached when heat flow through each layer of an object is equal
Convection #
- Heat flow by movement of mass
- Convection involves heat flowing by the bulk movement of molecules from one place to another
- Whereas conduction involved molecules/electrons moving over small distances, convection involves the movement of a large number of molecules over a long distance
- Natural Convection occurs in systems where a cold substance (air, water) is warmed and subsequently expands, decreasing density and thus rising
- Warm fluid/gases are less dense, thus they rise compared to colder fluid/gas
Radiation #
- Whereas conduction and convection require a medium, radiation doesn’t
- The sun’s rays are a form of heat and travel through (nearly empty) space
- Radiation of the sun’s rays arrive on a clear day at a rate around .$1000 \text{W/m}^2$
- Most of the time radiation consists of electromagnetic waves, but infrared (IR) wavelengths are responsible for heating Earth
- The sun’s rays are a form of heat and travel through (nearly empty) space
- The rate at which energy leaves a radiation object, .$Q/t$, is
$$ \frac{\Delta Q}{\Delta t} \varepsilon \sigma A T^4$$
- .$\varepsilon$ is called emissivity.
- Between 0 and 1
- Characteristic of the surface of the radiating material
- Black surfaces close to one, shiny metal surfaces close to zero
- Depends slightly on the temperature of the material
- A good absorber is also a good emitter
- A black tee shirt gets very hot because it absorbs nearly all the radiation that hits it
- .$\sigma$ is the Stefan-Boltzmann constant: .$\sigma = 5.67 \cdot 10^{-8} \text{ W/(m}^2 \text{K}^4\text{)}$
- .$\varepsilon$ is called emissivity.
- Objects also absorb heat of surrounding objects. This net heat flow can be found by
$$ \frac{\Delta Q}{\Delta t} \varepsilon \sigma A (T_1^4 - T_2^4)$$
- Where .$T_1$ is the object’s temperature and .$T_2$ is the surrounding environment’s temperature
- .$T_1 > T_2$: net flow of heat is from object to the surroundings
- .$T_1 < T_2$: net flow of heat is from surroundings into object, raising the object temperature