30.1 Mutual Inductance #

• When two wires are near one another, they induce an emf in one another
  • This emf is proportional to the rate of change of the flux passing through it
  • The flux passing through the coil is generated by the other coil’s current

• The emf induced in coil 2 due to a change in current 1 can be written now as $$\mathscr{E_2} = -N_2 \frac{d\Phi_{21}}{dt} = -M \frac{dI_1}{dt}$$

30.2 Self-Inductance; Inductors #

• This concept also applies to isolated coils too
  • When a changing current passes through a coil (or solenoid), a changing magnetic flux is produced inside the coil, and this in turn induces an emf in that same coil. This induced emf opposes the change in flux (Lenz’s law).
    • If the current through the coil is increasing, the increasing magnetic flux induces an emf that opposes the original current and tends to retard its increase.
    • If the current is decreasing in the coil, the decreasing flux induces an emf in the same direction as the current, thus tending to maintain the original current.
  • If this inductance (coil) is in a circuit, it thus can provide a source of emf, in addition to any battery present or other sources of emf.
• Self-inductance .$L$ and the emf it induces is given by

  $$L = \frac{N\Phi_B}{I}$$

  $$\mathscr{E} = -N \frac{d\Phi_B}{dt} = -L \frac{dI}{dt}$$

• An ac circuit always contains some inductance, but often it is quite small unless the circuit contains a coil of many loops or turns. A coil that has significant self-inductance .$L$ is called an inductor
  • Inductance can serve a useful purpose in certain circuits, but it’s often just a nuisance in a circuit.
  • If inductance is large, the change in the current will be small, and therefore the current itself if it is ac will be small.
    • The greater the inductance, the less the ac current.
    • An inductance thus acts something like a “resistance” to impede the flow of alternating current.

Solenoid Self-Inductance #

• The magnetic field of a solenoid is .$B = \mu_0 nI$ where .$n = N/l$
• Thus, the flux is .$\Phi_B = BA = \mu_0 NIA/l$ so we can derive $$L = \frac{N \Phi_B}{I} = \frac{\mu_0 N^2 A}{l}$$

30.3 Energy Stored in a Magnetic Field #

• When an inductor with inductance .$L$ is carrying current .$I$ which is changing at the rate .$dI/dt$, energy is being supplied to the inductor at the rate $$P = I \mathscr{E} = LI \frac{dI}{dt}$$
• Thus, the work needed to increase the current in an inductor from zero to some .$I$ is $$W = \int P dt = \int_0^I LI\ dI = \frac{1}{2}LI^2$$
  • This is also the (potential) energy stored in a conductor when it is carrying current .$I$
• Just as the energy stored in a capacitor can be considered to reside in the electric field between its plates, so the energy in an inductor can be considered to be stored in its magnetic field.
  • E.x. the energy stored in a solenoid is $$U = \frac{1}{2}LI^2 = \frac{1}{2} \bigg( \frac{\mu_0 N^2 A}{l} \bigg)\bigg( \frac{Bl}{\mu_0 N}\bigg)^2 = \frac{1}{2} \frac{B^2}{\mu_0}Al$$
  • We can think of this energy as residing in the volume enclosed by the windings; .$Al$
  • Then the energy density (energy per unit volume) is $$u = \text{energy density} = \frac{1}{2}\frac{B^2}{\mu_0}$$
    • This equation is analogous to that for an electric field, .$ \frac{1}{2}ϵE^2$

30.4 LR Circuits #

(a) LR circuit; (b) growth of current when connected to battery.

• At the instant the switch connecting the battery is closed, the current starts to flow.
  • It is opposed by the induced emf in the inductor because of the changing current. As soon as current starts to flow, there is also a voltage drop across the resistance; .$V = IR$
  • Hence, the voltage drop across the inductance is reduced and the current increases less rapidly as it approaches .$I_0 = V_0 / R$ as seen in (b)
• The emfs in the circuit are the battery voltage .$V_0$ and the emf .$\mathscr{E} = -L (dI/dt)$ in the inductor (which opposes the current)
  • Hence, we can find sum of potential charges around the loop where .$I$ is the current at any instance by using the loop rule: $$V_0 - IR - L \frac{dI}{dt} = 0 \Longrightarrow L \frac{dI}{dt} + RI = V_0$$
  • We can integrate the later term from .$t = 0, I = 0$ to a later time .$t$ when current is .$I$: $$\int_0^I \frac{dI}{V_0 - IR} = \int_0^t \frac{1}{L}dt \Longrightarrow - \frac{1}{R} \ln \bigg( \frac{V_0 - IR}{V_0} \bigg) \frac{t}{L}$$ $$\dots \Longrightarrow \frac{V_0 - IR}{V_0} = e^{- \frac{Rt}{L}} \Longrightarrow I = \frac{V_0}{R}(1-e^{-t/\tau})$$
    • .$\tau = \frac{L}{R}$ is the time constant: the time required for the current .$I$ to reach 63% of it’s maximum value .$V_0/R$

• When the battery is removed from the circuit…
  • Voltage .$V_0$ becomes zero, so .$L \frac{dI}{dt} + RI = 0$
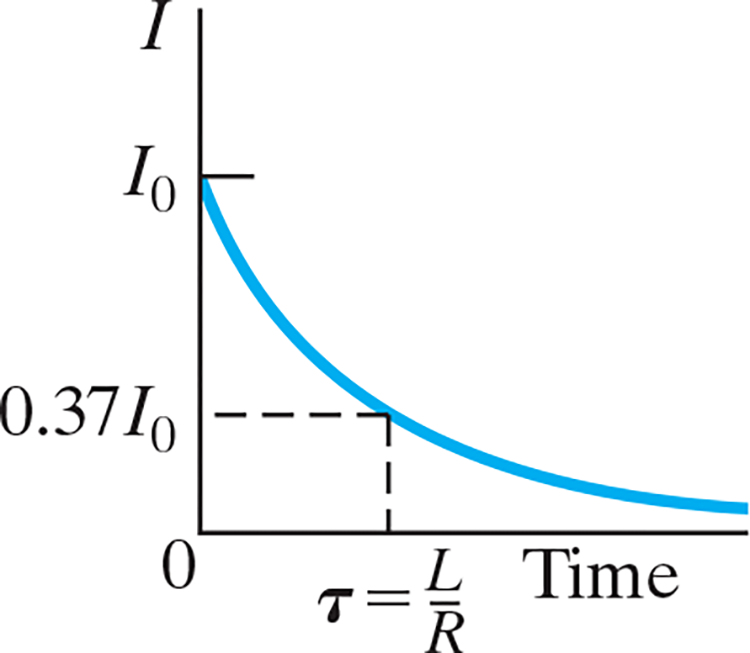
  • We can integrate this and solve for .$I$ $$\int_{I_0}^I \frac{dI}{I} = - \int_0^t \frac{R}{L} dt$$ $$\dots \Longrightarrow I = I_0 e^{-t/\tau}$$ - .$\tau = L/R$ is the time it takes current to decrease to 37% of it’s initial

30.5 LC Circuits and Electromagnetic Oscillations #

• Any electric circuit can contain the three basic components: resistance, capacitance, and inductance, in addition to a source of emf.

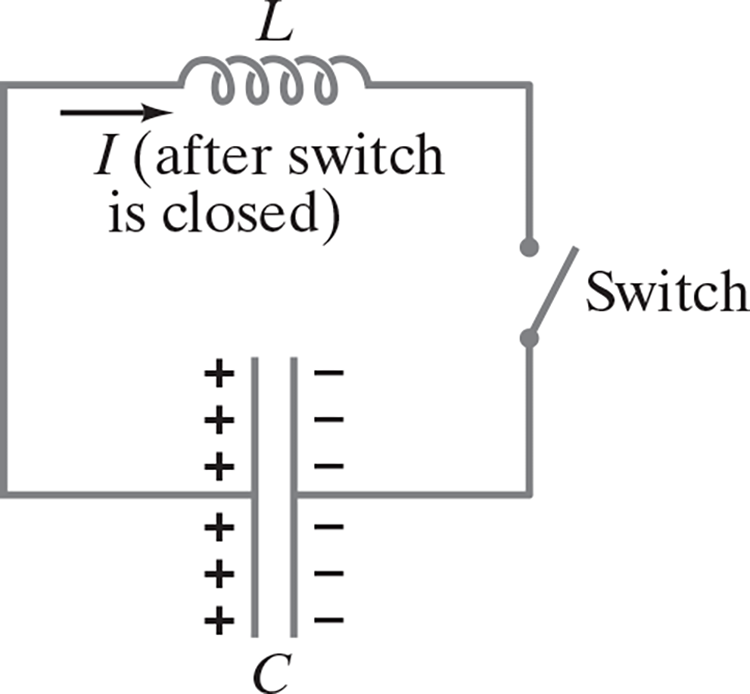
• Suppose the adjacent circuit is initially charged so one plate has charge .$Q_0$ and the other .$-Q_0$ and that the potential difference is .$V = Q/C$
• At .$t = 0$ the capacitor immediately begins to discharge. As it does so, the current .$I$ through the inductor increases. We now apply Kirchhoff’s loop rule (sum of potential changes around a loop is zero): $$-L \frac{dI}{dt} + \frac{Q}{C} = 0$$

• Because charge leaves the positive plate on the capacitor to produce the current .$I = dQ/dt$ so we can rewrite the equation as $$\dots \Longrightarrow \frac{d^2 Q}{dt^2} + \frac{Q}{LC} = 0 \Longrightarrow Q = Q_0 \cos(\omega t + \phi)$$
  • .$Q_0$ and .$\phi$ are constants that depend on the initial conditions
  • .$\omega t + \phi$ is in radians.
    • Because we have .$\phi$, the amplitude isn’t .$Q_0$ unless .$\phi = 0$
  • .$\omega = 2\pi f = \sqrt{ \frac{1}{LC} }$