17.1: Atomic Theory #
- Atoms are the smallest unit of matter
- Atomic unit: .$\text{u} = 1.66\cdot 10^{-27}$ kg
- E.x. Hydrogen weighs .$1.0078 \text{u}$
- Molecular mass of a compound is the sum of the particles (atoms) in the compound
Terms #
- Element: Substance that cannot be broken down into smaller substances (gold)
- Molecule: Group of atoms held together by covalent bonds
- Compound: Substance made from atoms combined in specific ratios
Brownian Motion #
- Random movement seen in pollen/dust, as well as atoms
- Using Brownian motion, Einstein found the size of an atom to be .$10^{-10}$ meters
Forces #
- Atoms and molecules exert an (electric) attractive force on one another by default
- If an atom/molecule gets too close to another, they exert a repelling force on one another
- Matter states:
- Solid:
- Atoms held in matrix formation by strong attractive forces.
- Atoms vibrate around their mean position
- Liquid:
- Force between atoms is weaker so atoms move more rapidly within
- Gas:
- Atom attractive forces are so weak compared to their kinetic energy that they move randomly
- If two atoms collide, the attractive force is so weak that they may just bounce off one another
- Solid:
17.2: Temperature and Thermometers #
- Matter property changes under different temperatures
- Sidewalks expand under the sun
- Electric resistance increases with heat
- Lightbulb filament glows
Thermometers Types #
- Originally used alcohol which expands linearly with heat (water doesn’t)
- Bimetalic strips bend at slightly different rates under heat
- Electronic thermometers measure resistance change and often have digital screens
Scales #
- Fahrenheit: Water freezes at 32 and boils at 212 deg
- Celsius: Water freezes at 0 and boils at 100 deg
- Kelvin: Celsius + 273.15K. Written without degree sign. Absolute = 0K
- Conversions: $$T(^\circ C) = \frac{5}{9}(T(^\circ F)-32)$$ $$T(^\circ F) = \frac{9}{5}(T(^\circ C)) + 32$$
- Different materials expand at different rates ro we use constant-volume thermos because it’s pressure linearly relates to the temperature
17.3 0th Law of Thermodynamics #
- If objects .$A$ and .$B$ are at equilibrium with object .$C$ , then .$A$ and .$B$ are also at equilibrium with one another
- Systems naturally reach equilibrium over time
Thermal Expansion #
- Most materials expand when heated
- Expansion amount depends on the material
- Equations (assuming a constant volume .$V$ )
- Linear Expansion:
- .$\alpha$ is the coefficient of linear expansion and depends on the material with units .$(^\circ C)^{-1}$ $$\Delta l \approxeq \alpha l_0 \cdot \Delta T$$ $$l_i + \Delta l = l_f = l_i ( 1 + \alpha\Delta T)$$ $$\frac{dl}{dT} = \alpha(T)\cdot l$$
- If .$\Delta T$ is too large such that the temperature dependence of .$\alpha$ is too large, we can do the following: $$\int_{l_i}^{l_f} \frac{1}{l}dl = \int_{T_i}^{T_f} \alpha(T) dT$$
- Volume Expansion:
$$\beta = \frac{1}{V} \frac{dV}{dT}$$
$$V_f \approxeq V_0 ( 1 + \beta\Delta T)$$
- .$\beta \approx 3\cdot\alpha$ = coefficient of volume expansion.
- Coefficient of expansion varies at extremely high heats so it only works with small .$\Delta T$ ’s
- Materials must be isotropic (have same expansion properties in all directions) for us to say .$\alpha \approx 3\cdot\beta$
- (Linear) expansion doesn’t exist for gas or liquids because they have no fixed space like solids.
- Linear Expansion:
- Weird water property
- .$0 - 4 ^\circ C$ : Water increases in density .$\rho^+\Longrightarrow$ decreases in volume .$V^-$
- .$4^\circ C +$ : Water acts “normally”: increase in volume .$V$ proportional to temperature .$T$
- This explains why pipes burst when frozen and why ice cubes float
17.5 Thermal Stresses #
- When the ends a solid (rod) are fixed (such as in beams), temperature changes induce thermal stress due to the clamp limiting expansion/contraction
- Process Steps:
- Beam tries to expand/contract by .$\Delta l$
- Mount reacts with an opposite reactive force, keeping it at it’s original length: $$\Delta l = \frac{1}{E} \cdot \frac{F}{A} \cdot l_0$$ where .$E$ is Young’s modulus for the material. We can also re-write for stress: $$\frac{F}{A} = \Delta l \cdot E \cdot \frac{1}{l_0} = (\alpha l_0 \Delta T) E \cdot \frac{1}{l_0} = \alpha E \Delta T$$
17.6 Gas Laws and Absolute Temperature #
- Equation at State describes how pressure varies with Temperature, Number of Particles (Molecules), and Volume
- State is the physical condition of a system
- Equilibrium State: .$T, N, \&\ V = \text{Constant}$
Laws #
- Assume that gasses aren’t too dense (so .$P \sim$ atmospheric pressure) and that they aren’t close to liquefaction (boiling) point either (for oxygen, this is .$~183^\circ \text{C}$.)
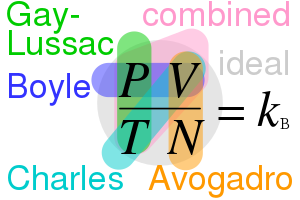
- Boyle’s Law
- .$V \propto P^{-1}$ [Constant Temperature]
- .$P$ is absolute, not gauge, pressure
- Alternatively, .$PV =$ const or .$P_1V_1 = P_2V_2$
- Charles’s Law
- .$V \propto T$ [Constant Pressure]
- Alternatively, .$\frac{V_1}{T_1} = \frac{V_2}{T_2}$
- Gay Lussac’s Law
- .$P \propto T$ [Constant Volume]
- Alternatively, .$\frac{P_1}{T_1} = \frac{P_2}{T_2}$
17.7 Ideal Gas Law #
$$PV = nRT = n k_B N_a T = N k_B T$$
- .$P$ is the pressure of the gas [Pascals]
- .$V$ is the volume of the gas [Cubic Meters]
- .$T$ is the absolute temperature of the gas [Kelvins]
- .$N$ is the number of molecules of gas
- .$n$ is the amount of substance of gas (number of moles) [Moles]
- .$R$ is the ideal, or universal, gas constant, equal to .$k_B \cdot N_a = 8.314 \frac{J}{K\cdot \text{mol}}$
- Using mass of a gas, different gasses have different proportionality constants
- So we used number of moles, in which case .$R$ becomes the constant for all gasses
- .$k_B $ is the
Boltzmann constant
- Relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas
- .$N_a$ is the
Avogadro constant
- The number of particles that are contained in one mole of gas
- .$n = N/N_A$
- This equation is Ideal in that the equation only works for gasses around atmospheric pressure and not excessive temperatures
Moles #
- Mole is the SI unit for amount of substance
- 1 mole = Number of particles in .$\text{12g}$ of Carbon
- 1 mole = Number of grams of a substance numerically equal to the molar mass $$n \text{(moles)} = \frac{\text{mass (grams)}}{\text{molecular mass (g/mol)}}$$
17.8 Problem Solving with .$PV = nRT$ #
STP: Standard Temperature and Pressure #
- .$T = 273 \text{K}$
- .$P = 1.00 \text{atm} = 1.013\cdot10^5 \text{N/m}^2 = 101.3 \text{kPA}$
- .$1 \text{mol of ideal gas} = 22.4\text{L}$ in volume
- If P is in liters and V is in atm, then we can use .$R = 0.0821 \frac{\text{L} \cdot \text{atm}}{\text{mol} \cdot \text{K}}$
- Since .$n$ and .$R$ are constants, we can say: $$\frac{P_1 V_1}{T_1} = \frac{P_2 V_2}{T_2}$$
17.9 Ideal Gas with Avogadro’s Number #
- Avogadro’s hypothesis:
- Equal volume of gas with the same .$P$ and .$T$ have an equal .$n$ umber of particles (molecules)
- .$N_a$ is avogadro’s number: the number of particles that are contained in one mole of gas (or one gram of hydrogen).
- .$N_a = 6.022 \cdot 10^{23}\ \text{particles/mole}$
- Therefore, if .$N$ is the number of molecules of a gas sample and .$n$ is the number of moles, then $$N = n\cdot N_A \Longrightarrow n = \frac{N}{N_A} \Longrightarrow PV = \frac{N}{N_A}RT = Nk_B T$$ where .$k_B $ is Boltzmann’s constant .$\frac{R}{N_A} = 1.38 \cdot 10^{-23} \frac{\text{J}}{\text{K}}$
17.10 Ideal Gas Temperature #
- Triple point: A precise temperature and pressure where the three phases (gas, liquid, and solid) of a substance can coexist in thermodynamic equilibrium.
- .$P_3 = 4.88\ \text{torr};\ T_3 = 0.01^\circ C$ for water
- Ideal Gas, constant volume: $$T = (273.16 K)\bigg(\frac{P}{P_3}\bigg)$$
- Constant volume: $$T = (273.16 K)\lim_{P_3 \to 0}\bigg(\frac{P}{P_3}\bigg)$$
A typical phase diagram. The solid green line applies to most substances; the dashed green line gives the anomalous behavior of water. For more see 18.4